因果關係怎麼研究?
在日常生活的經驗裡,我們往往習慣以主觀的角度來認定因果關係的存在,但在數理統計的協助下,因果關係可以擁有科學定義,並且可以驗證。中央研究院「研之有物」專訪院內統計科學研究所黃彥棕研究員,他的主要研究便是以數理統計的方式來探討因果關係(例如生物體的複雜機轉)。有了統計方法,人類也能接近上帝視角,找出因果關係的存在。
以數理統計驗證因果關係
我們絕大多數人相信「凡事必有因果」這句話,例如今天腹瀉,是因為昨天晚餐吃壞肚子;考試沒考好,是因為書念得不夠。但是仔細想想,造成今天拉肚子的原因,除了昨天的晚餐之外,還有沒有別的可能?影響考試成績的因素,除了書念得夠不夠之外,考試環境、考題難易度也都會影響。
所以,我們究竟該如何確定兩件事有因果關係?有沒有什麼科學方法,可以讓我們帶著十足的把握,說出「X 就是造成 Y 結果的原因」這樣的話語?
中研院統計所研究員黃彥棕,擅長以數理統計的方式來思考因果關係,除此之外他更進一步在數學上探討「X 透過何種機制造成 Y」,也就是所謂的「因果中介效應」。有興趣的讀者,可以參考「研之有物」之前專訪黃彥棕老師的文章〈喝酒臉紅易罹癌?小時候家裡窮會胖?統計學家黃彥棕來解答〉。
回到因果關係,黃彥棕說到:「因果關係是屬於上帝視角。」也就是說,兩件事之間究竟有無因果關係,理論上只有全知者才知道,而我們能做的,是以數理統計的方式,「從人類視角盡可能地逼近上帝視角,來判斷因果關係是否存在。」
何謂因果關係?
為什麼說「因果存在與否只有上帝才知道」?因果關係建立在「反事實」,如果有一個事實是「打疫苗,就不容易感染 COVID-19」,則我們必須驗證是否「不打疫苗,就容易感染 COVID-19」,這就是反事實。有了事實與反事實的比對,我們才能說「打疫苗」與「不易感染 COVID-19」有因果關係。
不過,除非有時光機或平行宇宙,否則我們不可能讓全世界的人打疫苗,並觀察感染情況;然後又讓全世界的人都不打疫苗,並再次觀察染病狀況。只有全知者才能同時觀察這兩個平行宇宙,得知因果關係。黃彥棕說,身處現實世界的我們,只能盡可能地逼近這個結果。
用數學語言來描述因果關係,最被廣泛使用的架構是由美國統計學家 Donald Rubin 提出的反事實結果(counterfactual outcome)或潛在結果(potential outcome)。值得一提的是,過去 Rubin 也曾與 2021 年諾貝爾經濟學獎得主 Joshua Angrist 和 Guido Imbens 共同發表重要論文〈使用工具變量確認因果效應〉。
以下我們就以疫苗和傳染病為例,
金旺線上娛樂城
以反事實架構來說明「X 導致 Y」的群體因果效應。先假設 X 為民眾施打疫苗與否( 0:不打疫苗,1:打疫苗),而 Y 為得傳染病與否(0:不染病,1:染病),並使用期望值 E 來描述群體平均效應,詳細如下圖。
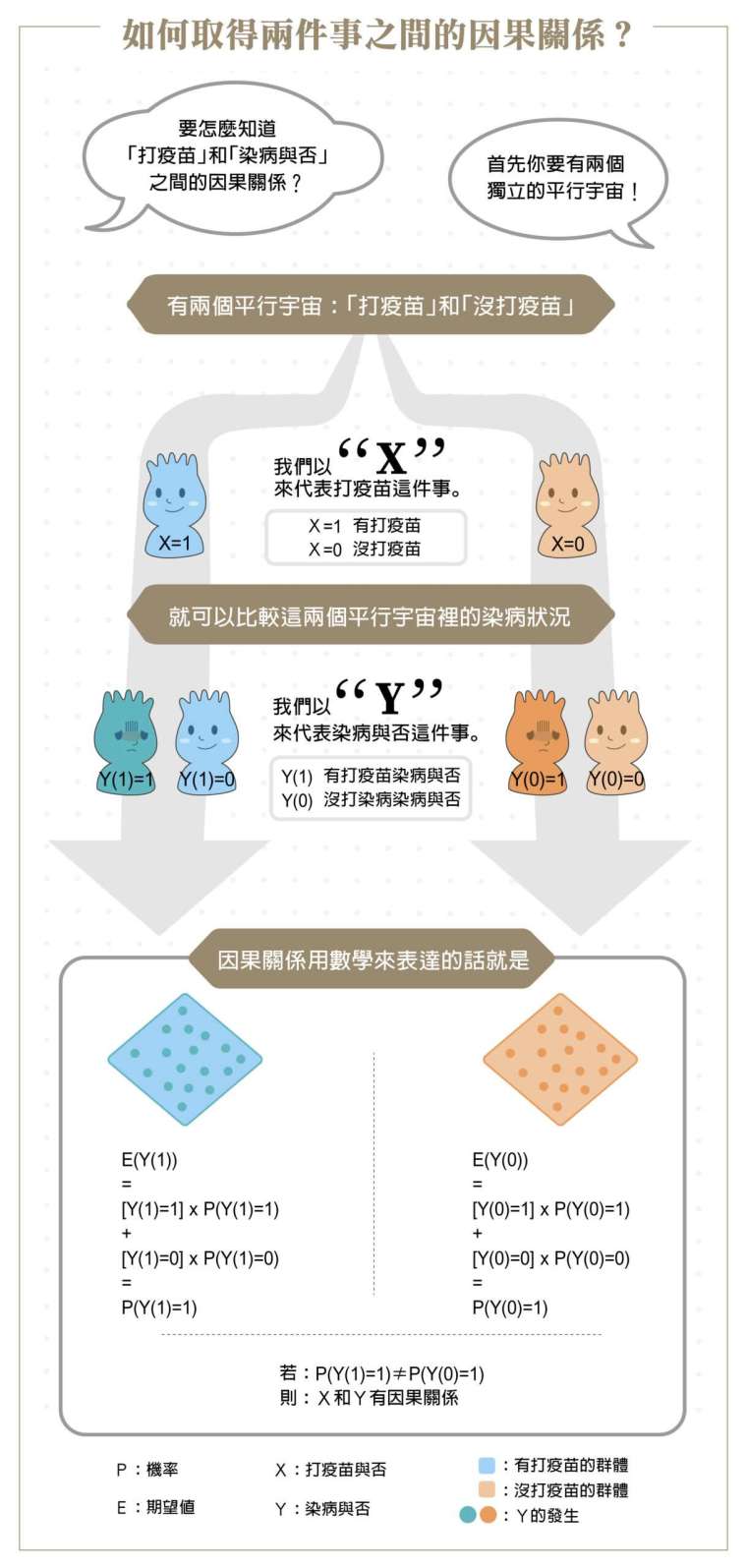
為了要取得因果關係,我們必須有兩個獨立的平行世界,分別是 X= 1 和 X=0,再去比較這兩個世界中 X 如何導致 Y 的發生。 圖│研之有物(資料來源│黃彥棕)
如果我們觀察到 E[Y(X=1)] = 0.1,也就是有打疫苗的人染病機率是 10 %。那麼在反事實因果推論的基礎上,我們必須檢驗 E[Y(X=0)] 等於多少,也就是不打疫苗的染病機率。只要 E[Y(X=1)] ≠ E[Y(X=0)],就代表 X 和 Y 之間具有因果關係。
然而,實務上打完疫苗的人不可能再回復到沒打疫苗的狀態,因此我們沒有辦法再次對同一群母體樣本做實驗來驗證因果關係,僅能退而求其次,「盡量貼近」因果關係。那麼,要怎麼做呢?
有反事實的對照,才有因果關係。
逼近神的因果視角
如果我們把全世界的人分成兩半,其中一半打疫苗、另一半不打疫苗,然後用打疫苗的那一半代表一個宇宙(事實),不打疫苗的代表另一個宇宙(反事實),不就創造出兩個平行宇宙了嗎?
這是一種很直觀的逼近方法,但若要讓一半的人能夠代表一整個宇宙,則有一個重要的前提:這兩個宇宙裡的人是隨機分配的,也就是這兩群人在各個層面都很相似,例如年齡、性別、健康狀況甚至政治傾向等,以專業術語來說就是必須具有可互換性(exchangeability)。藥廠在做疫苗人體實驗時,就必須以非常嚴謹的方式讓受試者盡可能達到隨機分配,才能得到「疫苗是否有效」的科學結果。
不過,在大多數狀況下,我們很難做到隨機分配。舉例來說,臺灣開放施打 COVID-19 疫苗後,截至 2021 年 10 月 29 日為止,有將近 1700 萬人施打第一劑疫苗,但我們不能把這 1700 萬人視為有打疫苗的宇宙,而另一群沒打疫苗的 600 萬人視為沒打疫苗的宇宙,因為打不打疫苗是人民自由選擇的結果,有很多因素會影響個人選擇,例如比較有健康意識,或是比較年輕、不擔心副作用的人,可能就比較傾向打疫苗。
即使統計結果顯示出打疫苗的人,感染 COVID-19 的比例真的比較低,我們也很難分辨是因為打疫苗,還是他們本來就比較年輕?或本來就比較健康?「這是所謂的『觀察型研究』,容易出現因果推論謬誤的原因。」黃彥棕說。
然而,我們可以用數理統計的方式逼近真實的因果效應,例如控制年齡、健康狀況──兩方都取 50-60 歲的年齡層,並且都是沒有心血管疾病的人等。黃彥棕說:「我們依據自己的背景知識,知道有哪些因素會影響隨機性,然後使用統計的方式,把它們抓出來做控制。」
理論上統計學家可以把所有可能造成偏誤的因子都舉出來,透過一層層地篩選、限縮,最後得出許多個小小的族群,讓隨機性成立。
之後,透過每一組小小的隨機族群(例如年齡 50-60 歲、沒有心血管疾病、男性、具健康意識…… 等,
DG試玩
統稱為 C),讓 Y 的發生和特定條件 C 之下的 X 群體無關,我們就可以得到逼近兩個平行宇宙的資料(有打疫苗、沒打疫苗),最後再把各族群的結果加權平均回來。就可以貼近上帝視角的因果效應。
以數學語言來說,就是讓條件期望值(E[Y|X=x, C=c)])的計算透過加權平均等同於反事實結果之期望值(E[Y(X=x)])的效果。我們沒有時光機,無法透過事實/反事實結果之期望值檢驗全體打疫苗和不打疫苗的因果關係(E[Y(X=1)] ≠ E[Y(X=0)] 嗎?);但是我們可以透過各種條件的篩選和限縮,去計算每個具備可互換性小群體的條件期望值,最後加權平均回來,檢視打疫苗與得病與否的因果關係(∑c E[Y|X=1, C=c]*P(C=c) ≠ ∑c E[Y|X=0, C=c]*P(C=c) 嗎?),這才是實務上的作法。
問題來了,
淘金娛樂城
要怎麼知道我們是否窮舉了所有可能造成偏誤的因子?我們的確不知道,只有上帝知道,這是個假設,而且是個很難驗證的假設。
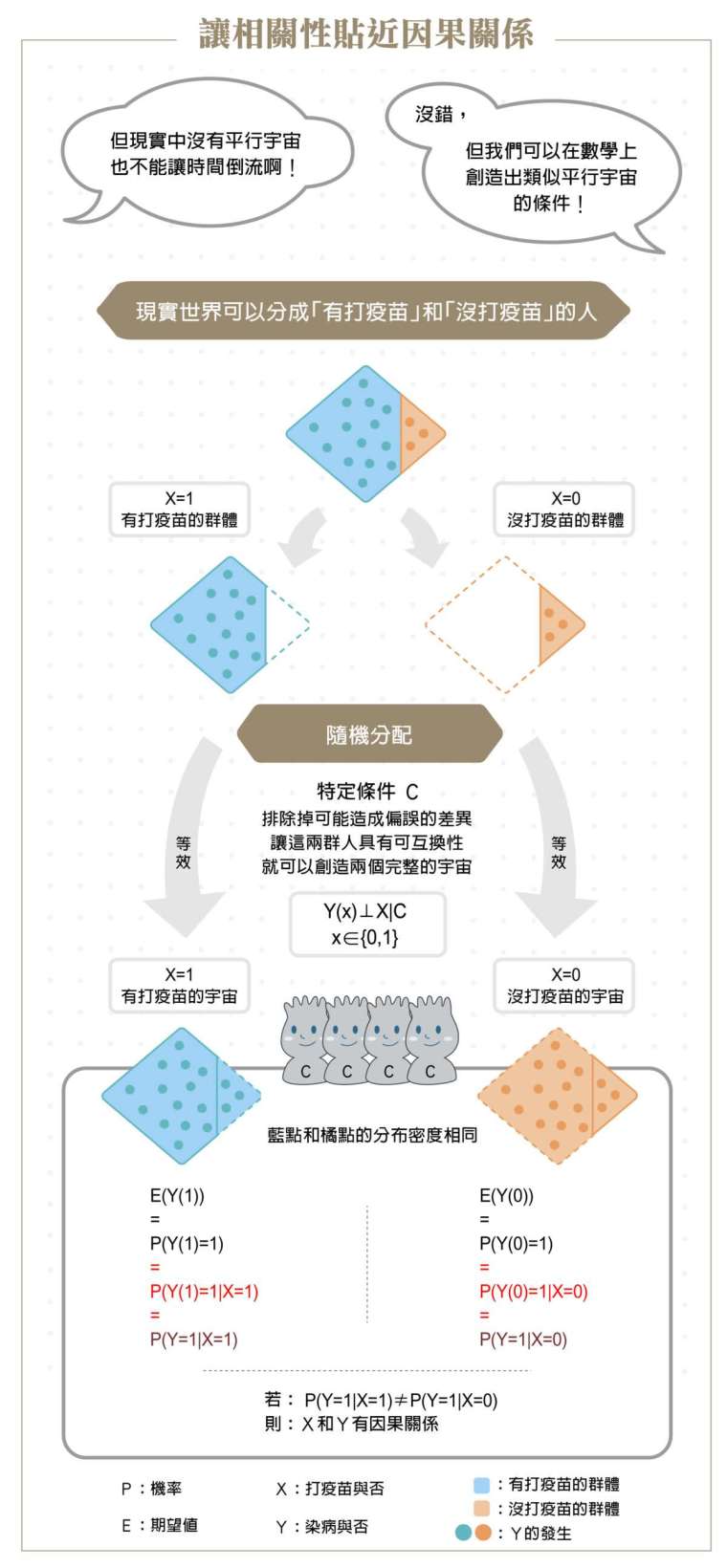
實務上,我們不可能同時觀察 X= 1 和 X=0 的世界,只能分別獲得 X 和 Y 的相關性。要如何從相關性去檢視因果關係呢?透過統計學上的篩選和限制,我們如果可以讓 X=1 vs. X=0 的隨機性成立,就可以進一步驗證 X 和 Y 的因果關係。為方便說明,圖片的數學式為簡單條件期望值計算,
5298線上娛樂
不考慮加權平均。 圖│研之有物(資料來源│黃彥棕)
「在控制了年齡、性別、健康狀況等條件的情況下,我們希望可以讓隨機性成立。」
黃彥棕的研究讓因果關係在嚴謹的數學架構下,得以辨證、溝通,而不是只仰賴直觀的思考。因果的存在變得更加科學化,而這也使因果的探討可以進入更深的層次。
被競爭結果和時間擾亂的因果關係
更進階的因果探討層次,是將時間因素考慮進來。黃彥棕以「B 型肝炎」造成「肝癌」,然後導致「死亡」為例,
雷火體育
若想探討這三者間的因果關係時,會發生一個問題,那就是有 B 型肝炎的人,有可能容易因猛爆性肝炎而直接死亡,而這樣的個案在統計上,因為他並沒有得到肝癌,而對「肝癌」這個中介因子造成了「保護」的效果。
「這就是肝癌和死亡這兩個競爭結果造成的影響,而這個競爭關係又會隨著時間推移而改變。肝癌、死亡有時間進程關係,
色碟
一旦 B 型肝炎患者因猛爆性肝炎死亡了,他就不可能再得肝癌。」更清楚地說,B 型肝炎患者可能還「來不及」得肝癌,就因猛爆性肝炎直接跳到死亡。在界定 B 型肝炎與肝癌之間的因果關係時,這樣的結果會造成偏誤。
黃彥棕將時間因素考慮進來的方法,是把整個時程切割成非常多小段,在每個小段創造一個反事實架構,也就是分析每一位在某小段時間活著的 B 型肝炎患者,把他們分成已得到肝癌及還沒得到肝癌,並考慮這兩組患者在下一個瞬間死亡的可能性,再將這些結果積分起來,得到在隨機過程架構之下的平行宇宙們。
「我等於是在每一個瞬間都製造多個平行宇宙(無 B 肝/無肝癌、無 B 肝/有肝癌、有 B 肝/無肝癌、有 B 肝/有肝癌)出來,這樣做可以避免前面說的蓋牌效應。但你可以想像我所得到的平行宇宙數量…… 嗯,就跟《奇異博士》看到的差不多。」
「我認為我在這領域的部分貢獻,或許是提出了這樣一個會隨著時間推移的反事實架構。」黃彥棕說。他的論文發表出來後不久,也引起了期刊的興趣,邀請了相關領域的許多專家,探討他所提出的因果模型。
研究因果的動機
談起對因果關係研究的動機,黃彥棕說,以前在醫學系實習時,會看到開同樣的藥給病人,有些病人會好,有些人不會。這種「不確定性」開始讓他覺得好奇。他說:「我可以接受事情就是會有隨機性,但還是很想搞清楚這樣的不確定性是怎麼來的。」
最近,黃彥棕也發現許多人會把「預測」和「因果」搞混,尤其是現在人工智慧(AI)發展出的預測模型表現愈來愈好,有些做 AI 預測模型的人,會誤以為能夠用預測表現良好的模型,來得到因果關係。
舉例來說,一個模型可以透過一個人是否抽菸,來預測他得肺癌的機率,也可以透過一個人身上是否攜帶著打火機,來預測肺癌機率。「但我們知道抽菸與肺癌有因果關係,而帶打火機與否應該是不會造成任何增加肺癌風險的生物效應的。」黃彥棕說。
「抽菸」與「帶打火機」都能成為 AI 模型預測肺癌時採用的因子,但顯然並非代表它們與肺癌都有因果關係。黃彥棕接著說:「雖然預測未必需要因果關係,但是,決策就需要因果關係的支持。若要降低肺癌風險,政府較合理的做法是下令禁菸,而不是禁打火機。但要看到因果是比較困難的,它先天上的限制使它難以驗證,這個挑戰也是因果推論的迷人之處。」
最後,黃彥棕切身感受到因果關係的重要性,尤其是藥廠研發藥物或是臨床醫學等領域的應用。而他在反事實架構上考慮時間因素的突破,讓因果推論的知識又更往前推進。反事實因果推論的數學模型,讓人類能夠有深刻的思考,去檢視深藏在直觀表面之下的因果性與相關性。
原文連結:如何用數學探討因果關係?先學會處理無限多個平行宇宙吧!
延伸閱讀:
Huang, Y. T. (2021). Causal mediation of semicompeting risks. Biometrics, 77(4), 1143–1154.
Jaeger, D. A. (2021, October 19). Nobel economics prize winners showed economists how to turn the real world into their laboratory. The Conversation. Retrieved May 18, 2022.
黃彥棕(2021)。〈淺談因果:是宗教,是哲學,也是科學〉,《中研院訊》。
簡鈺璇(2020)。〈補習有用嗎?反事實分析的發現可能和你想的不一樣〉,《科技大觀園》。
林婷嫻(2019)。〈喝酒臉紅易罹癌?小時候家裡窮會胖?統計學家黃彥棕來解答〉,《研之有物》。
黃彥棕(2019)。〈因果中介模型〉,《自然科學簡訊》,31(1): 24-28。
文章源自於鉅亨新聞,














